今天在实现一个小功能 “插入更新 ListBox 中的 Item ”时,发现 ListBox.Items 的类型 ListBox.ObjectCollection 实现了 IList, ICollection, IEnumerable三个接口,整体的方法已经非常接近一个数组,但是方便程度跟数据确实差距较大,Linq 也完全不能使用,故封装一个扩展方法实现直接获取 ListBox.Items中所储存的数据的集合。
编写高质量C#程序的建议(1-5)
最近开始阅读陆敏技先生在机械工业出版社出版的《编写高质量代码:改善C#程序的157个建议》一书,打算把其中涉及的所有的观点做一下总结和分析,用于总结和事后翻阅,如果有侵权请联系我删除。
建议一:正确操作字符串
确保尽量小的装箱
在自己编写的代码中,应当尽可能地避免编写不必要的装箱代码。
1 | var str1 = "str1" + 9; |
第一句代码中,+ 连接时是将 值类型 int 转换为 引用类型 string 之后在进行 Concat 操作,故而性能更差。
装箱之所以带来性能损耗的原因是,装箱需要以下三个步骤:
- 首先,会为值类型在托管堆中分配内存。除了值类型本身所分配的内存外,内存总量还要加上类型对象指针和同步块索引所占用的内存。
- 将值类型的值复制到新分配的堆内存中。
- 返回已经成为引用类型的对象的地址。
避免分配额外的内存空间
频繁的进行字符串的拼接操作时,最好使用 StringBuilder,字符串的任何方法或者进行任何运算都会在内存中创建一个新的字符串对象。
建议二:使用默认转型方法
- 使用类型的转换运算符。
- 使用类型内置的 Parse、TryParse,或者如 ToString、ToDouble 和 ToDateTime 等方法。
- 使用帮助类提供的方法。
- 使用 CLR 支持的转型
建议三:区别对待强制转型与 as 和 is
- 如果类型之间都上溯到了某个共同的基类,那么根据此基类进行的转型(即基类转型为子类本身)应该使用 as。子类与子类之间的转型,则应该提供转换操作符,以便进行强制转型。
- as 操作符永远不会抛出异常,如果类型不匹配则会返回 null。
- as 不能操作基元类型,如果涉及基元类型的算法,就需要通过 is 转型前的类型进行判断,以避免转型失败。
- C# 7.0 中提供了 is 的新语法,以下两个方法其实是完全等价的:
1
2
3
4
5
6
7
8
9
10
11
12public void A2(object obj)
{
var str = obj as string;
if (str != null)
Console.WriteLine(str);
}
public void A3(object obj)
{
if (obj is string str)
Console.WriteLine(str);
}
建议四: TryParse 比 Parse 好
Parse 和 TryParse 如果执行成功,他们的效率在一个数量级上,但如果执行失败,Parse 方法在转化失败的时候会引发异常,极大地消耗效率,而 TryParse 并不会。
建议五: 使用 int? 来确保值类型也可以为 null
业务需求中,int 类型的字段在无意义时在业务上为 null 比它的默认值 0 更为合适。
关于租房到期离职纠结
如何判定一个类型支不支持 await 异步等待(代码)
最近由于一些业务上的需求,需要在 OnActionExcutionAsync 和 OnActionExcuted 中判断当前请求的接口是否是异步的接口,刚好前几天看过吕毅大佬的文章《.NET 中什么样的类是可使用 await 异步等待的?》,遂封装实现一下判断类型是否为可等待类型的方法。
聚会合租选点:计算距离多个地铁站点综合时间最少的聚会地点
使用不安全代码 + 反射修改 String.Empty 的值
前几天的时候看到了 吕毅 大佬写的博客
为什么 C# 的 string.Empty 是一个静态只读字段,而不是一个常量呢?,
非常感谢吕毅大佬的分享,在文章的末尾大佬提到了通过反射修改 String.Empty 的可能,于是我打算自己实践一下。
记一次失败平衡车破解提速之旅
bash脚本错误 Syntax error: else unexpected (expecting then)解决
今天在使用 bash 脚本发布程序时,发生了这样的错误
1 | xxx.sh: Syntax error: "else" unexpected (expecting "then") |
到处搜索资料尝试无果之后想到会不会是编码问题导致,
dos2unix 处理后测试果然可以
【微服务学习】Polly:熔断降级组件
【微服务学习】Consul 服务治理发现
Consul 服务治理发现
简介
Consul 是 HashiCorp 公司推出的开源工具,用于实现分布式系统的服务发现与配置。与其他分布式服务注册与发现的方案,Consul的方案更“一站式”,内置了服务注册与发现框架、分布一致性协议实现、健康检查、Key/Value存储、多数据中心方案,不再需要依赖其他工具(比如ZooKeeper等)。使用起来也较为简单。Consul使用Go语言编写,因此具有天然可移植性(支持Linux、windows和Mac OS X);安装包仅包含一个可执行文件,方便部署,与Docker等轻量级容器可无缝配合 。
- service discovery:consul通过DNS或者HTTP接口使服务注册和服务发现变的很容易,一些外部服务,例如saas提供的也可以一样注册。
- health checking:健康检测使consul可以快速的告警在集群中的操作。和服务发现的集成,可以防止服务转发到故障的服务上面。
- key/value storage:一个用来存储动态配置的系统。提供简单的HTTP接口,可以在任何地方操作。
- *multi-datacenter:无需复杂的配置,即可支持任意数量的区域。
Consul 是注册中心,服务提供者、服务消费者等都要注册到 Consul 中,这样就可以实现服务提供者、服务消费者的隔离。
除了 Consul 之外,还有 Eureka、Zookeeper、Etcd 等类似服务发现框架。
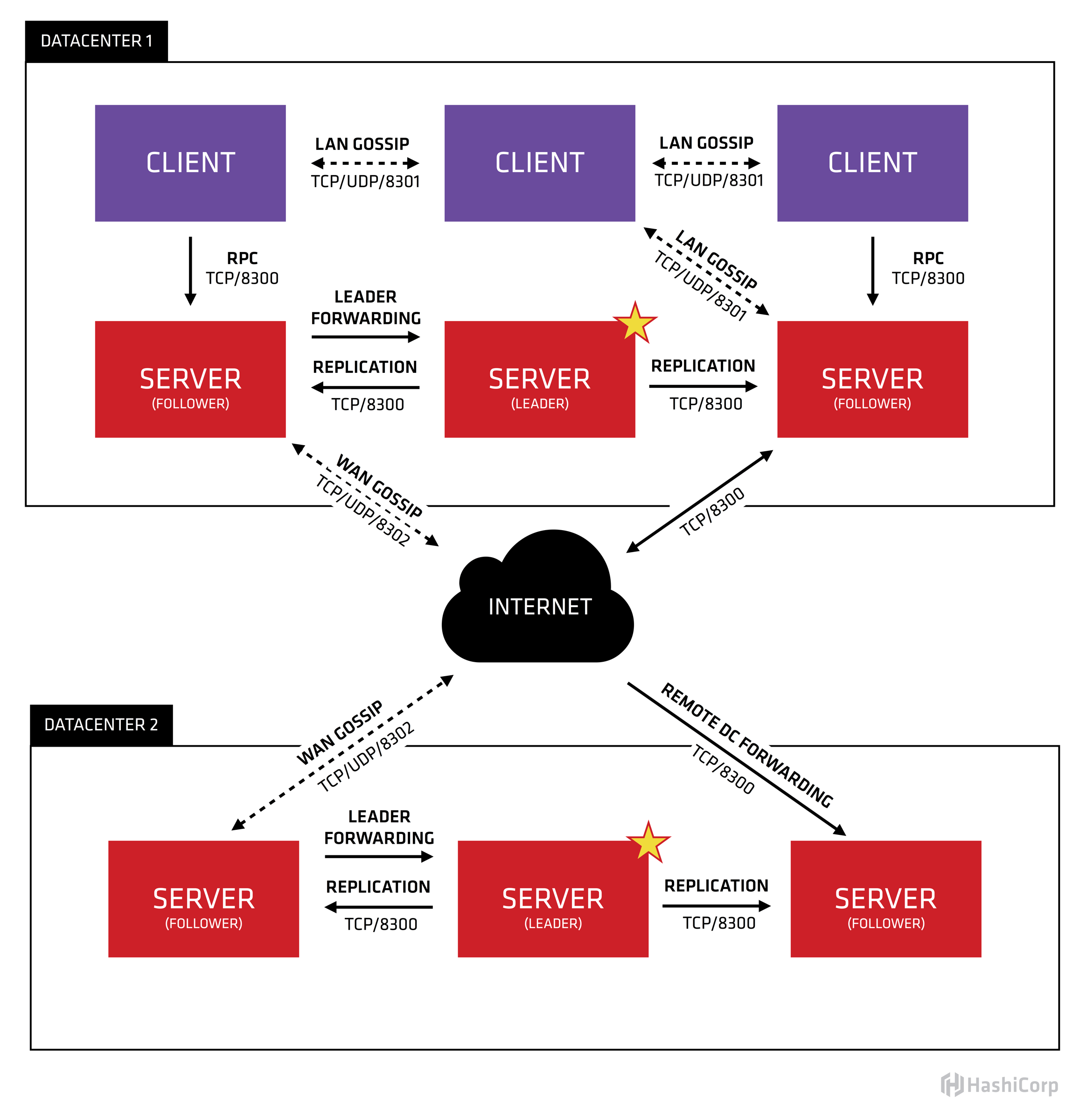
Consul 相关概念
CLIENT
CLIENT表示consul的client模式,就是客户端模式。是consul节点的一种模式,这种模式下,所有注册到当前节点的服务会被转发到SERVER,本身是不持久化这些信息。SERVER
SERVER表示consul的server模式,表明这个consul是个server,这种模式下,功能和CLIENT都一样,唯一不同的是,它会把所有的信息持久化的本地,这样遇到故障,信息是可以被保留的。SERVER-LEADER
中间那个SERVER下面有LEADER的字眼,表明这个SERVER是它们的老大,它和其它SERVER不一样的一点是,它需要负责同步注册的信息给其它的SERVER,同时也要负责各个节点的健康监测。其它信息
其它信息包括它们之间的通信方式,还有一些协议信息,算法。它们是用于保证节点之间的数据同步,实时性要求等等一系列集群问题的解决。这些有兴趣的自己看看官方文档。
我的理解
Consul 的整体功能其实就类似于互联网中的 DNS 服务器,Consul 服务端根据客户端传入的服务名,返回所有提供该服务的地址,整个流程跟 DNS 服务器将域名转化为 IP 地址有异曲同工之妙。
Consul 在 .NET Core 下的实践
我是用的开发平台是 Windows 64bit,鉴于 Windows 使用 Docker 的繁琐和诸多问题,以下流程直接下载运行 Consul 而不使用 Docker。
下载安装运行
- 从Consul 下载页面下载对应平台的最新版本的 Consul 程序并解压。
![]()
![]()
- 运行 consul.exe agent -dev (使用开发模式进行测试,如需生产环境集群使用,只要需要一台 Server,多台 Agent)
![]()
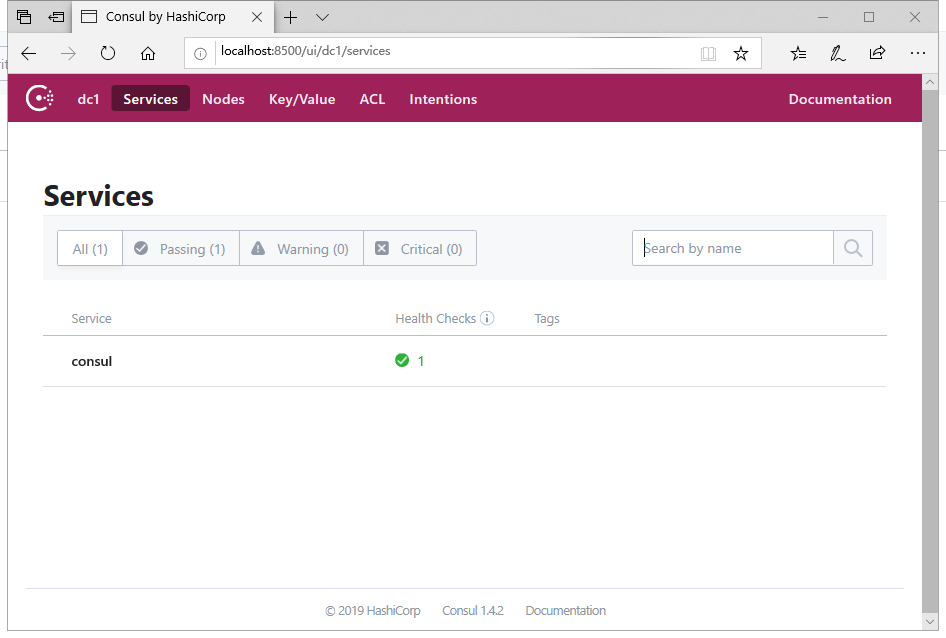
- 访问自带的 Web 后台查看即时信息
![]()
.NET Core 下的 Consul 实践
Install-Package Consul
程序与 Consul 的交互主要有三种:
- 服务注册
- 服务查询
- 服务健康检查
服务注册与反注册
随机获取一个可用端口
1 | using System; |
Program 增加属性 CurrentPort
1 | public static IWebHostBuilder using ConsulDemo.Extensions; |
将注册与反注册的方法绑定到生命周期的开始和结束
1 | public void Configure(IApplicationBuilder app, IHostingEnvironment env, IApplicationLifetime lifetime) |
结果视图
启动五个服务提供程序,图中可以看得到连接成功后的打印以及 Consul 健康检查得请求日志。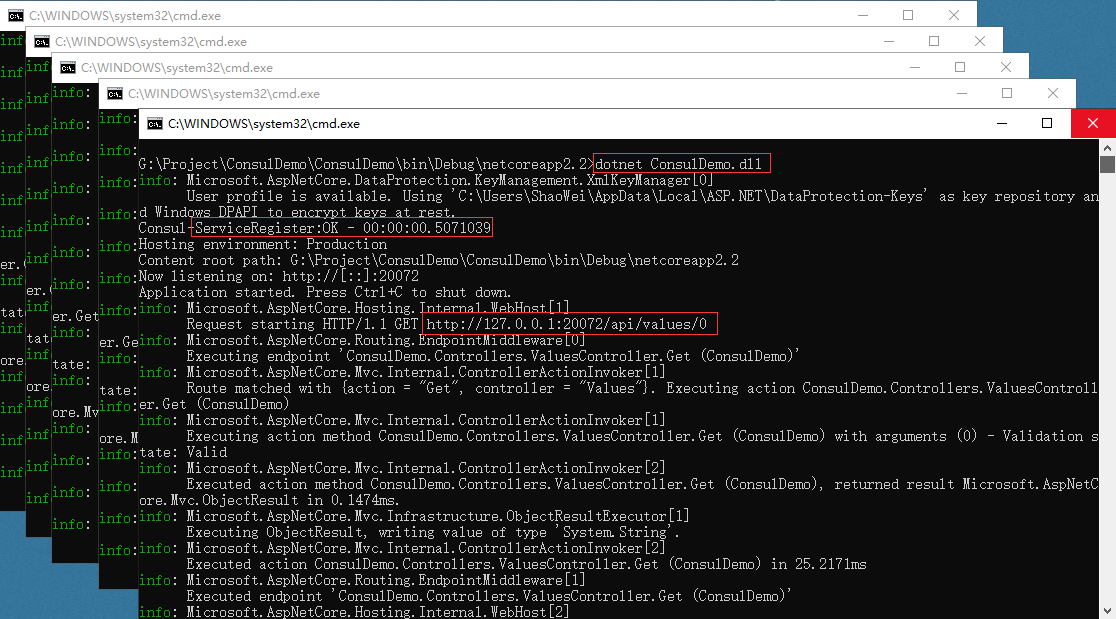
从 Consul 的后台可以清楚的看到已经成功注册了五个 ConsulDemo 服务提供程序。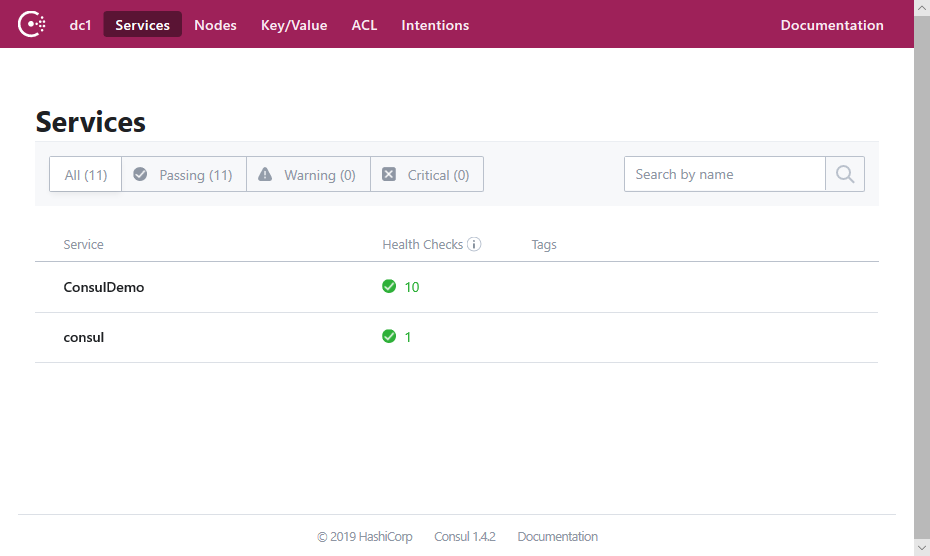
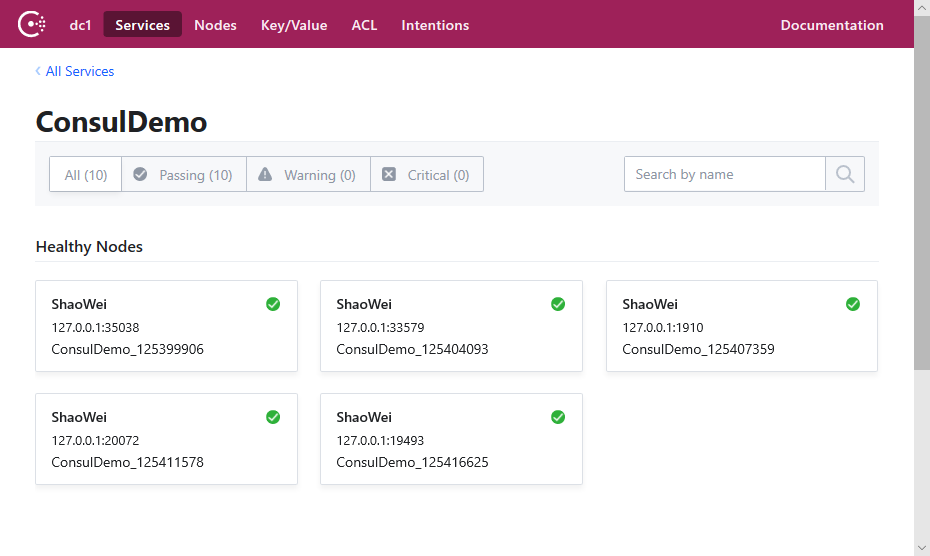
服务消费程序
首先我们新建一个 RestTemplate
RestTemplate(模仿 Spring Cloud 中的)
1 | using Consul; |
调用代码
1 | static void Main(string[] args) |
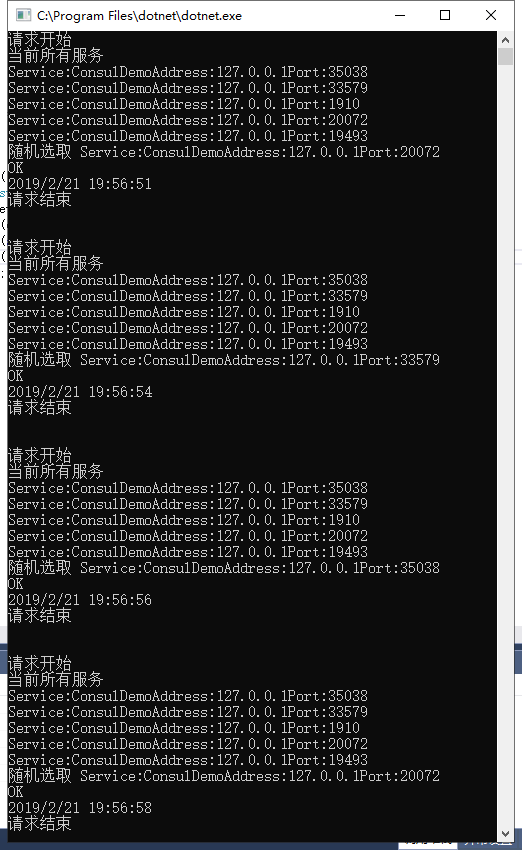
手动关掉一个服务端
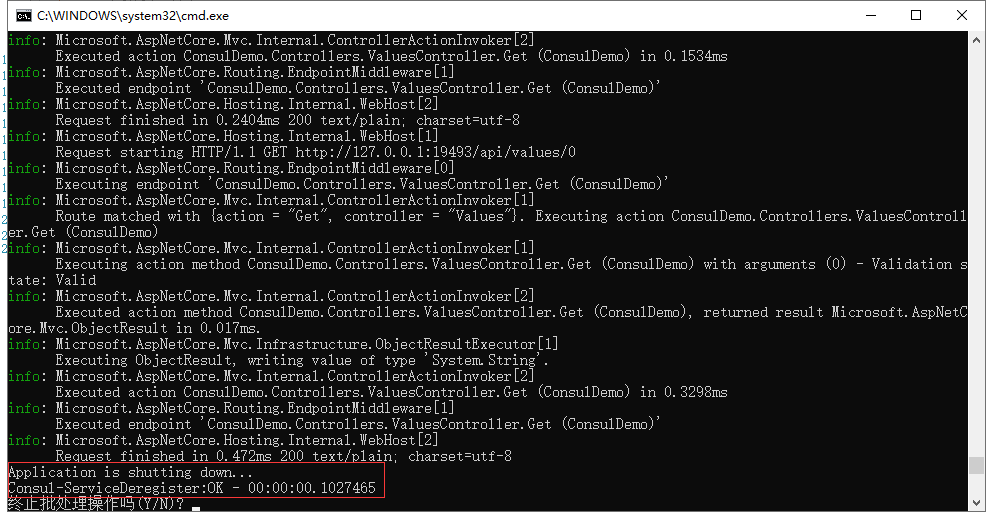
关掉的程序成功消失(反注册)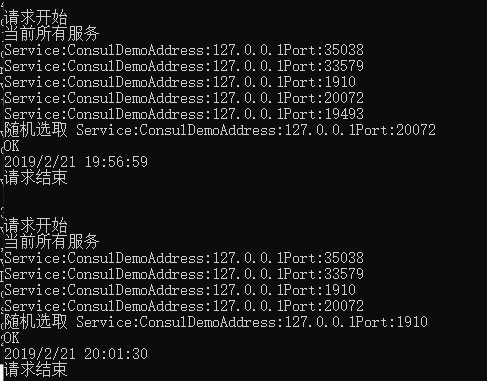
资源管理器杀掉一个程序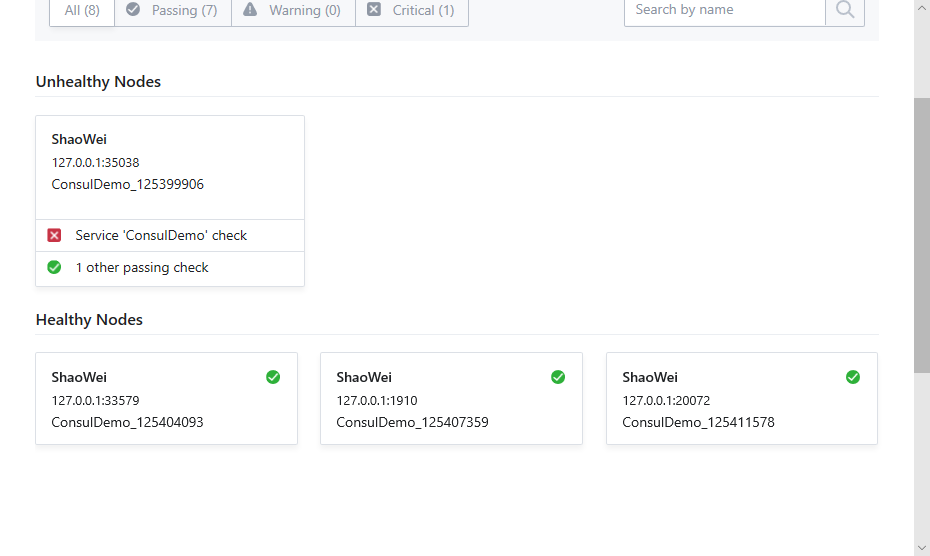
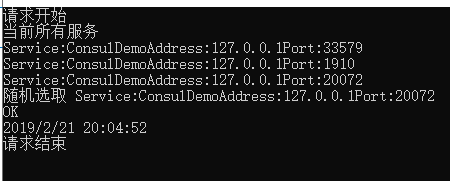
源码 ConsulDemo.7z